| CSparseMatrixGeneric< _Field, _Row, VectorCategories::SparseAssociativeVectorTag >::_IndexedIterator< RepIterator, RowIdxIterator, _I_Element > | No doc |
| CBCSR | Block CSR |
| CBitVector | Binary constant defined both for 32 and 64 bits |
| ►CBlackboxArchetype | Showing the member functions provided by all blackbox matrix classes |
| CMatrixBlackbox< _Field, _Matrix, _Vector > | Matrix black box |
| ►CBlackboxBlockContainerBase< _Field, _Blackbox, _MatrixDomain > | A base class for BlackboxBlockContainer |
| CBlackboxBlockContainerRecord< _Field, _Blackbox, _MatrixDomain > | No doc |
| CBlackboxBlockContainerBase< Field, Blackbox, _MatrixDomain > | |
| CBlackboxContainerBase< Field, Blackbox > | A base class for BlackboxContainer |
| ►CBlackboxContainerBase< Field, _Blackbox > | |
| CBlackboxContainer< Field, _Blackbox, RandIter > | Limited doc so far |
| CBlackboxContainerSymmetric< Field, _Blackbox, RandIter > | See base class for doc |
| CBlackboxContainerSymmetrize< Field, _Blackbox, RandIter > | Symmetrizing iterator (for rank computations) |
| ►CBlackboxContainerBase< Field, Vector > | |
| CDenseContainer< Field, Vector, RandIter > | Limited doc so far |
| CBlackboxFactory< Field, Blackbox > | A tool for computations with integer and rational matrices |
| ►CBlasMatrix< _Field, _Storage > | Dense matrix representation |
| CTransposedBlasMatrix< TransposedBlasMatrix< Matrix > > | TransposedBlasMatrix |
| CTriangularBlasMatrix< _Field, _Storage > | Triangular BLAS matrix |
| CBlasMatrix< _Field > | |
| CBlasMatrix< Domain > | |
| CBlasMatrix< Field > | |
| CBlasMatrix< Field, typename LinBox::Vector< Field >::Dense > | |
| CBlasMatrix< Givaro::Modular< double > > | |
| CBlasMatrix< Givaro::ZRing< Element > > | |
| CBlasMatrix< MultiModDouble > | No Doc |
| CBlasMatrix< typename _Matrix::Field, typename _Matrix::Rep > | |
| CBlasMatrixDomain< Field_ > | Interface for all functionnalities provided for BlasMatrix |
| CBlasMatrixDomain< Field > | |
| CBlasMatrixDomainAddin< Field, Operand1, Operand2 > | C += A |
| CBlasMatrixDomainMulAdd< BlasVector< Field >, BlasMatrix< Field, _Rep >, BlasVector< Field > > | What about subvector/submatrices ? |
| CBlasMatrixDomainSubin< Field, Operand1, Operand2 > | C -= A |
| CBlasPermutation< _UnsignedInt > | Lapack-style permutation |
| CBlasPermutation< size_t > | |
| CBlasSubmatrix< _Matrix > | Dense Submatrix representation |
| ►CBlasSubmatrix< BlasMatrix< _Field > > | |
| CSubmatrix< BlasMatrix< _Field >, VectorCategories::DenseVectorTag > | Specialization for BlasMatrix |
| CBlockBB< _BB > | Converts a black box into a block black box |
| CBlockCompose< _Blackbox1, _Blackbox2 > | Blackbox of a product: 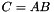 , i.e , i.e 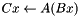 |
| CBlockCoppersmithDomain< _Domain, _Sequence > | Compute the linear generator of a sequence of matrices |
| CBlockHankelLiftingContainer< _Ring, _Field, _IMatrix, _FMatrix, _Block > | Block Hankel LiftingContianer |
| CBlockLanczosSolver< Field, Matrix > | Block Lanczos iteration |
| CBlockMasseyDomain< _Field, _Sequence > | Compute the linear generator of a sequence of matrices |
| CBlockMasseyDomain< Field, LinBox::BlackboxBlockContainerRecord > | |
| CBlockWiedemannLiftingContainer< _Ring, _Field, _IMatrix, _FMatrix > | Block Wiedemann LiftingContianer |
| CBooleanSwitch | Boolean switch object |
| CButterfly< _Field, Switch > | Switching Network based BlackBox Matrix |
| CCekstvSwitch< Field > | The default butterfly switch object |
| CChineseRemainder< CRABase > | No doc |
| CChineseRemainderSequential< CRABase > | No doc |
| CClassifyRing< Field > | Default ring category |
| CCommentator | Give information to user during runtime |
| CCompanion< Field_ > | Companion matrix of a monic polynomial |
| CCompose< _Blackbox1, _Blackbox2 > | Blackbox of a product: 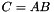 , i.e , i.e 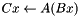 |
| CCompose< _Blackbox, _Blackbox > | Specialization for _Blackbox1 = _Blackbox2 |
| CCompose< LinBox::Submatrix< Blackbox >, LinBox::Transpose< LinBox::Submatrix< Blackbox > > > | |
| CCompose< LinBox::Transpose< LinBox::Submatrix< Blackbox > >, LinBox::Submatrix< Blackbox > > | |
| CComposeOwner< _Blackbox1, _Blackbox2 > | Blackbox of a product: 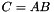 , i.e , i.e 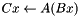 |
| CComposeTraits< IMatrix > | Used in ..., for example |
| CComposeTraits< BlasMatrix< Field, Rep > > | Used in smith-binary, for example |
| CBlasSubmatrix< _Matrix >::ConstIndexedIterator | Raw Indexed Iterator (const version) |
| CBlasSubmatrix< _Matrix >::ConstIterator | Raw Iterators (const version) |
| CContainerCategories | Used to separate BLAS2 and BLAS3 operations |
| CContainerTraits< Container > | Trait for the Category |
| CContainerTraits< std::vector< _Rep > > | |
| CCOO | Cordinate |
| CCOO1 | Implicit value COO (with only ones, or mones, or..) |
| ►CCRABuilderFullMultip< Domain_Type > | Chinese remaindering of a vector of elements without early termination |
| CCRABuilderEarlyMultip< Domain_Type > | NO DOC |
| CCRABuilderFullMultipFixed< Domain_Type > | Chinese Remaindering Algorithm for multiple residues |
| CCRABuilderFullMultipMatrix< Domain_Type > | NO DOC |
| CCRABuilderFullSingle< Domain_Type > | Chinese Remaindering with full precision and no chance of failure |
| ►CCRABuilderSingleBase< Domain_Type > | Abstract base class for CRA builders |
| ►CCRABuilderEarlySingle< Domain_Type > | Heuristic Chinese Remaindering with early termination |
| CCRABuilderEarlyMultip< Domain_Type > | NO DOC |
| CCRABuilderProbSingle< Domain_Type > | Chinese Remaindering with guaranteed probability bound and early termination |
| CCRAResidue< ResultType, Function > | Type information for the residue in a CRA iteration |
| CCRAResidue< Integer, Function > | Type information for the residue in a CRA iteration |
| CCRAResidue< std::vector< Integer >, Function > | Type information for the residue in a CRA iteration |
| CCSF< _Field > | Space efficient representation of sparse matrices |
| CCSR | Compressed row |
| CCSR1 | Implicit value CSR (with only ones, or mones, or..) |
| CDataSeries | This structure holds a bunch of timings |
| CDenseMat< _Element > | To be used in standard matrix domain |
| ►CDenseMat< SlicedBase< _Domain::Word_T > > | |
| CSliced< _Domain > | The Sliced Matrix class _Domain must be a GF(3) rep, BaseT must be an unsigned int type |
| CDensePolynomial< Field > | Dense Polynomial representation using Givaro |
| CDeterministicTag | Iterator following a deterministic sequence of primes (from the largest one, in decreasing order |
| CDIA | Diagonal |
| CDiagonal< Field, Trait > | Random diagonal matrices are used heavily as preconditioners |
| CDiagonal< _Field, VectorCategories::DenseVectorTag > | Specialization of Diagonal for application to dense vectors |
| CDiagonal< _Field, VectorCategories::SparseAssociativeVectorTag > | Specialization of Diagonal for application to sparse associative vectors |
| CDiagonal< _Field, VectorCategories::SparseSequenceVectorTag > | Specialization of Diagonal for application to sparse sequence vectors |
| CDiagonal< Field > | |
| CDif< _Blackbox1, _Blackbox2 > | Blackbox of a difference: C := A - B, i.e Cx = Ax - Bx |
| CDiophantineSolver< QSolver > | DiophantineSolver<QSolver> creates a diophantine solver using a QSolver to generate rational solutions |
| CDirectSum< _Blackbox1, _Blackbox2 > | If C = DirectSum(A, B) and y = xA and z = wB, then (y,z) = (x,w)C |
| CDirectSum< Companion< Field_ > > | |
| CDixonLiftingContainer< _Ring, _Field, _IMatrix, _FMatrix > | Dixon Lifting Container |
| CDotProductDomain< Givaro::Modular< uint16_t, Compute_t > > | Specialization of DotProductDomain for unsigned short modular field |
| CDotProductDomain< Givaro::Modular< uint32_t, Compute_t > > | Specialization of DotProductDomain for uint32_t modular field |
| CDotProductDomain< Givaro::Modular< uint64_t, Compute_t > > | Specialization of DotProductDomain for uint64_t modular field |
| CDotProductDomain< Givaro::Modular< uint8_t, Compute_t > > | Specialization of DotProductDomain for unsigned short modular field |
| CDotProductDomain< Givaro::ModularBalanced< double > > | Specialization of DotProductDomain |
| ►CElementAbstract | Abstract element base class, a technicality |
| CElementEnvelope< Ring > | |
| CElementEnvelope< Field > | Adaptor from archetypical interface to abstract interface, a technicality |
| CElementArchetype | Field and Ring element interface specification and archetypical instance class |
| CEliminator< Field, Matrix > | Elimination system |
| CEliminator< Field, LinBox::BlasMatrix > | |
| CELL | Ellpack |
| CELL_R | Ellpack fixed row |
| ►CException | This is the exception class in LinBox |
| CalgoException | Algorithmic exception |
| CBadInputException | The input is not as expected |
| CIrrecuperableException | Something bad an unexpected happened |
| CNotImplementedYetException | Not implemented yet |
| ►CFieldAbstract | Field base class |
| ►CFieldEnvelope< Ring > | |
| CRingEnvelope< Ring > | Implement the ring archetype to minimize code bloat |
| CFieldEnvelope< Field > | Derived class used to implement the field archetypeHelps to minimize code bloat |
| ►CRingAbstract | Abstract ring base class |
| CRingEnvelope< Ring > | Implement the ring archetype to minimize code bloat |
| CFieldAXPY< Field > | FieldAXPY object |
| CFieldAXPY< Field_ > | |
| CFieldAXPY< GF2 > | |
| CFieldAXPY< Givaro::Modular< double > > | |
| CFieldAXPY< Givaro::Modular< float > > | |
| CFieldAXPY< Givaro::Modular< int16_t > > | |
| CFieldAXPY< Givaro::Modular< int32_t, Compute > > | |
| CFieldAXPY< Givaro::Modular< int64_t, Compute_t > > | |
| CFieldAXPY< Givaro::Modular< int8_t > > | |
| CFieldAXPY< Givaro::Modular< uint16_t, Compute_t > > | Specialization of FieldAXPY for uint16_t modular field |
| CFieldAXPY< Givaro::Modular< uint32_t, Compute_t > > | Specialization of FieldAXPY for unsigned short modular field |
| CFieldAXPY< Givaro::Modular< uint64_t, Compute_t > > | Specialization of FieldAXPY for unsigned short modular field |
| CFieldAXPY< Givaro::Modular< uint8_t, Compute_t > > | Specialization of FieldAXPY for uint8_t modular field |
| CFieldAXPY< Givaro::ModularBalanced< double > > | Specialization of FieldAXPY |
| CFieldAXPY< Givaro::ModularBalanced< float > > | |
| CFieldAXPY< Givaro::ModularBalanced< int32_t > > | |
| CFieldAXPY< Givaro::ModularBalanced< int64_t > > | |
| CFieldAXPY< LinBox::ParamFuzzy > | |
| CFieldAXPY< PIR_ntl_ZZ_p > | |
| CFieldAXPY< PIRModular< int32_t > > | |
| CFieldAXPY< Ring > | |
| ►CFieldDocumentation | This field base class exists solely to aid documentation organization |
| ►CFieldArchetype | Field specification and archetypical instance |
| CRingArchetype | Specification and archetypic instance for the ring interfaceThe RingArchetype and its encapsulated element class contain pointers to the RingAbstract and its encapsulated ring element, respectively |
| CParamFuzzy | Abstract parameterized field of "fuzzy" doubles |
| CFieldTraits< Field > | FieldTrait |
| ►CGaussDomain< _Field > | Repository of functions for rank by elimination on sparse matrices |
| CPowerGaussDomain< _Field > | Repository of functions for rank modulo a prime power by elimination on sparse matrices |
| CGaussDomain< Field > | |
| CGenericRandIter< Field > | Random field base element generator |
| ►CGenericTag | Generic ring |
| CGaloisTag | Galois Field GF(p^e) |
| CIntegerTag | If it is isomorphic to Z |
| CModularTag | If it is isomorphic to Z/mZ, for some m or its extensions |
| CRationalTag | If it is isomorphic to Q |
| ►CVectorCategories::GenericVectorTag | Generic vector (no assumption is made) |
| ►CVectorCategories::SparseVectorTag | Sparse vectors (general) |
| CVectorCategories::SparseAssociativeVectorTag | Sparse vectors (general) |
| CVectorCategories::SparseParallelVectorTag | Sparse vectors (general) |
| CVectorCategories::SparseSequenceVectorTag | Sparse vectors (general) |
| ►CVectorCategories::SparseZeroOneVectorTag | Sparse GF2 vectors |
| ►CVectorCategories::DenseVectorTag | Dense vector (GF2 and general) |
| CVectorCategories::DenseZeroOneVectorTag | Sparse vectors (general) |
| CGetEntryCategory< BB > | GetEntryCategory is specialized for BB classes that offer a local getEntry |
| CGivaroRnsFixedCRA< Domain_Type > | NO DOC.. |
| CGmpRandomPrime | Generating random prime integers, using the gmp library |
| CGMPRationalElement | Elements of GMP_Rationals |
| CHeuristicTag | Iterator sampling randomly (no distribution guaranteed whatsoever) from all primes of given bitsize |
| CHilbert_JIT_Entry< _Field > | The object needed to build a Hilbert matrix as a JIT matrix |
| CHom< Source, Target, Enabled > | Map element of source ring(field) to target ringAn instance of Hom is a homomorphism from a ring of type Source to a ring (usually field) of type Target |
| CHom< Source, Target > | |
| CHYB | Hybrid |
| CInconsistentSystem< Vector > | Exception thrown when the system to be solved is inconsistent |
| CindexDomain | Class used for permuting indices |
| CIndexedCategory< BB > | Trait to show whether or not the BB class has a Indexed iterator |
| CIndexedCategory< BlasMatrix< Field, _Rep > > | |
| CBlasMatrix< _Field, _Storage >::IndexedIterator | Indexed Iterator |
| CBlasSubmatrix< _Matrix >::IndexedIterator | Raw Indexed Iterator |
| CSparseMatrix< _Field, SparseMatrixFormat::CSR >::IndexedIterator | Forward iterator |
| CZeroOne< GF2 >::IndexedIterator | IndexedIterator |
| CZeroOne< _Field >::IndexIterator | IndexIterator |
| CInverse< Blackbox > | A Blackbox for the inverse |
| CInverse< LinBox::Compose< LinBox::Submatrix< Blackbox >, LinBox::Transpose< LinBox::Submatrix< Blackbox > > > > | |
| CInverse< LinBox::Compose< LinBox::Transpose< LinBox::Submatrix< Blackbox > >, LinBox::Submatrix< Blackbox > > > | |
| CInvertTextbookDomain< Field > | Assumes that Field is a field, not a ring |
| CBlasSubmatrix< _Matrix >::Iterator | Raw Iterators |
| CZeroOne< _Field >::Iterator | Raw iterator |
| CZeroOne< GF2 >::Iterator | Raw iterator |
| CJIT_Matrix< _Field, JIT_EntryGenerator > | Example of a blackbox that is space efficient, though not time efficient |
| ►CJIT_Matrix< _Field, Hilbert_JIT_Entry< _Field > > | |
| CHilbert< _Field > | Example of a blackbox that is space efficient, though not time efficient |
| CPoint::Labels | X |
| CLABlockLanczosSolver< Field, Matrix > | Biorthogonalising block Lanczos iteration |
| CLanczosSolver< Field, Vector > | Solve a linear system using the conjugate Lanczos iteration |
| CLargeDouble | NO DOC |
| CLastInvariantFactor< _Ring, _Solver > | This is used in a Smith Form algorithm |
| ClatticeMethod | NTL methods |
| CLIL | Vector of pairs |
| CLinboxError | Base class for execption handling in LinBox |
| CLocal2_32 | Fast arithmetic mod 2^32, including gcd |
| CMasseyDomain< Field, Sequence > | Berlekamp/Massey algorithm |
| CMatrixArchetype< _Element > | Directly-represented matrix archetype |
| CMatrixCategories | For specializing matrix arithmetic |
| CMatrixContainerTrait< Matrix > | NODOC |
| CMatrixDomain< GF2 > | Specialization of MatrixDomain for GF2 |
| CMatrixHomTrait< Blackbox, Field > | Try to map a blackbox over a homorphic ring The most suitable type |
| CMatrixPermutation< _UnsignedInt > | Permutation classique |
| CMatrixRank< _Ring, _Field, _RandomPrime > | Compute the rank of an integer matrix in place over a finite field by Gaussian elimination |
| CMatrixStream< Field > | MatrixStream |
| CMatrixStreamReader< Field > | An abstract base class to represent readers for specific formats |
| CMatrixTraits< Matrix > | NO DOC |
| ►CMetaData | This is the general metadata class |
| CAlgorithmMetaData | Algorithm metadata; |
| CBenchmarkMetaData | Benchmark metadata; |
| CEnvironmentMetaData | Environment metadata; |
| CFieldMetaData | Field metadata |
| CGeneratorMetaData | Generator metadata; |
| CMatrixMetaData | Matrix metadata |
| CStorageMetaData | Storage metadata; |
| CMethod | Define which method to use when working on a system |
| CMethodBase | Holds everything a method needs to know about the problem |
| CMGBlockLanczosSolver< Field, Matrix > | Block Lanczos iteration |
| CModularCrookedRandIter< Element > | Random field base element generator |
| CMoorePenrose< Blackbox > | Generalized inverse of a blackbox |
| ►CMVProductDomain< Field > | Helper class to allow specializations of certain matrix-vector products |
| CMatrixDomain< Domain > | |
| CMatrixDomain< Field > | |
| CMatrixDomain< Givaro::Modular< double > > | |
| CMatrixDomain< PolynomialRing > | |
| CMatrixDomain< Ring > | |
| ►CMVProductDomain< Field_ > | |
| CMatrixDomain< Field_ > | Class of matrix arithmetic functions |
| CMVProductDomain< Givaro::Modular< uint16_t, Compute_t > > | Specialization of MVProductDomain for uint16_t modular field |
| CMVProductDomain< Givaro::Modular< uint32_t, Compute_t > > | Specialization of MVProductDomain for uint32_t modular field |
| CMVProductDomain< Givaro::Modular< uint64_t, Compute_t > > | Specialization of MVProductDomain for uint64_t modular field |
| CMVProductDomain< Givaro::Modular< uint8_t, Compute_t > > | Specialization of MVProductDomain for uint8_t modular field |
| Cnaive | Toom-Cook method |
| CNoHomError | Error object for attempt to establish a Hom that cannot exist |
| CNTL_ZZ | Integer ring |
| ►CNTL_zz_p | Long ints modulo a positive integer |
| CNTL_PID_zz_p | Extend Wrapper of zz_p from NTL |
| ►CNTL_ZZ_p | Wrapper of zz_p from NTL |
| CPIR_ntl_ZZ_p | Extend Wrapper of ZZ_p from NTL |
| CNTL_ZZ_pE | Wrapper of ZZ_pE from NTL Define a parameterized class to handle easily Givaro::ZRing<NTL::ZZ_pE> field |
| ►CNTL_zz_pE_Initialiser | Use ZZ_pEBak mechanism too ? |
| CNTL_zz_pE | Zz_pE Define a parameterized class to easily handle Givaro::ZRing<NTL::zz_pE> field |
| CNTL_zz_pEX | Ring (in fact, a unique factorization domain) of polynomial with coefficients in class NTL_zz_p (integers mod a wordsize prime) |
| CNTL_zz_pX | Ring (in fact, a unique factorization domain) of polynomial with coefficients in class NTL_zz_p (integers mod a wordsize prime) |
| CNTL_ZZ_pX | Ring (in fact, a unique factorization domain) of polynomial with coefficients in class NTL_ZZ_p (integers mod a wordsize prime) |
| CNullMatrix | This is a representation of the 0 by 0 empty matrix which does not occupy memory |
| COneInvariantFactor< _Ring, _LastInvariantFactor, _Compose, _RandomMatrix > | Limited doc so far |
| COpenCLEnviron | Container for all pertenant information needed to use an OpenCL device, compile kernels for the device, track resource usage, and gain exclusive access to the device |
| COpenCLMatrixDomain< Field_ > | Interface for all functionnalities provided for BlasMatrix using GPUs |
| CPair< I, T > | Pair of I and T : struct { column index, value } |
| CPlainSubmatrix< MatDom > | To be used in reference matrix domain (PlainDomain) |
| CPlainSubmatrix< Domain_ > | |
| CPlotStyle::Plot | What style of graphic : histogram ? graph ? |
| CPlotData | The raw data to plot |
| CPlotGraph | The graph (2D) |
| CPlotStyle | Represents a table of values to plot (2D) |
| CPLUQMatrix< Field > | PLUQ factorisation |
| CPoint::Points | Numerical value for x |
| CPolynomialBB< Blackbox, Poly > | Represent the matrix P(A) where A is a blackbox and P a polynomial |
| CPolynomialBBOwner< Blackbox, Poly > | Represent the matrix P(A) where A is a blackbox and P a polynomial |
| CPolynomialRing< BaseRing, StorageTag > | Polynomials |
| CPowerGaussDomainPowerOfTwo< UnsignedIntType > | Repository of functions for rank modulo a prime power by elimination on sparse matrices |
| CPreconditionFailed | A precondition failed |
| ►CPrimeIterator< Trait > | Prime Iterator |
| CMaskedPrimeIterator< Trait > | Masked Prime Iterator |
| CChineseRemainderSequential< CRABase >::PrimeSampler< PrimeIterator, is_unique > | Helper class to sample unique primes |
| CChineseRemainderSequential< CRABase >::PrimeSampler< PrimeIterator, true > | Helper class to sample unique primes |
| CPrimeSequence< IteratorT, UniqueTrait > | Adaptor class to make a fixed-length sequence behave like a PrimeIterator |
| CPrimeStream< Element > | Prime number stream |
| ►CRandIterAbstract | Random field element generator |
| CRandIterEnvelope< Field > | Random field base element generator |
| CRandIterArchetype | Random field element generator archetype |
| CRandomDenseMatrix< Randiter, Field > | Random Dense Matrix builder |
| CRankBuilder | Random method for constructing rank |
| CRationalChineseRemainder< RatCRABase > | Chinese remainder of rationals |
| CRationalChineseRemainderVarPrec< RatCRABase, RatRecon > | Chinese remainder of vector of rationals |
| CRationalReconstruction< _LiftingContainer, RatRecon > | Limited doc so far |
| CRationalSolver< Ring, Field, RandomPrime, MethodTraits > | Interface for the different specialization of p-adic lifting based solvers |
| CRationalSolver< Ring, Field, RandomPrime, Method::BlockHankel > | Block Hankel |
| CRationalSolver< Ring, Field, RandomPrime, Method::BlockWiedemann > | Partial specialization of p-adic based solver with block Wiedemann algorithm |
| CRationalSolver< Ring, Field, RandomPrime, Method::Dixon > | Partial specialization of p-adic based solver with Dixon algorithm |
| CRationalSolver< Ring, Field, RandomPrime, Method::SparseElimination > | Sparse LU |
| CRationalSolver< Ring, Field, RandomPrime, Method::SymbolicNumericNorm > | Solver using a hybrid Numeric/Symbolic computation |
| CRationalSolver< Ring, Field, RandomPrime, Method::Wiedemann > | Partial specialization of p-adic based solver with Wiedemann algorithm |
| CRawVector< Element > | Canonical vector types |
| ►CRawVector< Field ::Element > | |
| CVector< Field > | |
| ►CRawVector< Ring::Element > | |
| CVector< Ring > | Vector ?? |
| CBlasMatrix< _Field, _Storage >::rebind< _Tp1 > | Rebind operator |
| CRebind< XXX, U > | Used in support of Hom, MatrixHom |
| CRebind< std::vector< T >, U > | Rebind |
| CReverseVector< Vector > | Reverse vector class This class wraps an existing vector type and reverses its direction |
| CRingInterface | This ring base class exists solely to aid documentation organization |
| CRNS< Unsigned > | RNS |
| CScalarMatrix< Field_ > | Blackbox for aI |
| CSemiDIteration< Matrix, Field > | CRA iteration to get a diagonal with the same signature |
| CshowProgression | Show progression on the terminal (helper) |
| CSigmaBasis< _Field > | Implementation of 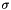 -basis (minimal basis) -basis (minimal basis) |
| CSlicedPolynomialMatrixAddin< Field, Operand1, Operand2 > | C += A |
| CSlicedPolynomialMatrixSubin< Field, Operand1, Operand2 > | C -= A |
| CSlicedPolynomialVectorAddin< Field, Operand1, Operand2 > | C += A |
| CSlicedPolynomialVectorSubin< Field, Operand1, Operand2 > | C -= A |
| CSmithFormBinary< _Ring, _oneInvariantFactor, _Rank > | Compute Smith form |
| CSmithFormIliopoulos | This is Iliopoulos' algorithm to diagonalize |
| CSmithFormLocal< LocalPID > | Smith normal form (invariant factors) of a matrix over a local ring |
| CSMM | Sparse Map of Maps |
| CSparse_Vector< T, I > | Vector< Pair<T,I> > and actualsize |
| CSparseLULiftingContainer< _Ring, _Field, _IMatrix, _FMatrix > | SparseLULiftingContainer |
| CSparseMap | Pair of vector/list (Pair of Containers) |
| CSparseMatrix< _Field, SparseMatrixFormat::COO > | Sparse matrix, Coordinate storage |
| CSparseMatrix< _Field, SparseMatrixFormat::COO::implicit > | Sparse matrix, Coordinate storage |
| CSparseMatrix< _Field, SparseMatrixFormat::CSR > | Sparse matrix, Coordinate storage |
| CSparseMatrix< _Field, SparseMatrixFormat::ELL > | Sparse matrix, Coordinate storage |
| CSparseMatrix< _Field, SparseMatrixFormat::ELL_R > | Sparse matrix, Coordinate storage |
| CSparseMatrix< _Field, SparseMatrixFormat::HYB > | Sparse matrix, Coordinate storage |
| CSparseMatrix< Field_, SparseMatrixFormat::TPL > | Sparse Matrix in Triples storage |
| CSparseMatrix< Field_, SparseMatrixFormat::TPL_omp > | Sparse matrix representation which stores nonzero entries by i,j,value triples |
| CSparseMatrixGeneric< _Field, _Row, Trait > | Sparse matrix container This class acts as a generic row-wise container for sparse matrices |
| CSparseMatrixGeneric< _Field, _Row > | |
| CSparseMatrixGeneric< _Field, Vector< _Field >::SparseMap > | |
| CSparseMatrixGeneric< _Field, Vector< _Field >::SparseMap, VectorCategories::SparseAssociativeVectorTag > | |
| CSparseMatrixGeneric< _Field, Vector< _Field >::SparsePar > | |
| CSparseMatrixGeneric< _Field, Vector< _Field >::SparsePar, VectorCategories::SparseParallelVectorTag > | |
| CSparseMatrixGeneric< _Field, Vector< _Field >::SparseSeq > | |
| CSparseMatrixGeneric< _Field, Vector< _Field >::SparseSeq, VectorCategories::SparseSequenceVectorTag > | |
| CSparseMatrixReadHelper< Matrix > | Read helper |
| CSparseMatrixWriteHelper< Matrix > | Write helper |
| CSparsePar | Vector/list of pairs (Container of Maps) |
| CSparseSeq | Vector/list of pairs (Container of Pairs) |
| CSquarize< Blackbox > | Transpose matrix without copying |
| CSubiterator< Iterator > | Subvector iterator class provides striding iterators |
| CSubiterator< _blasRep::iterator > | |
| CSubiterator< _Vector::Rep::iterator > | |
| CSubiterator< typename Rep::const_iterator > | |
| CSubiterator< typename Rep::iterator > | |
| CSubmatrix< Blackbox, Trait > | Leading principal minor of existing matrix without copying |
| CSubmatrix< Blackbox > | |
| ►CSubmatrix< Blackbox, VectorCategories::DenseVectorTag > | Specialization for dense vectors |
| CSubmatrix< Blackbox, VectorCategories::DenseZeroOneVectorTag > | Specialization for dense ZeroOne vectors |
| CSubmatrixAdapter< _Matrix > | Generic submatrix view adapter used internally in the OpenCLMatrixDomain |
| CSubmatrixOwner< Blackbox, VectorCategories::DenseVectorTag > | Specialization for dense vectors |
| CSubvector< Iterator, ConstIterator > | Dense subvectorThis class provides a statically sized subvector of a random access container (such as std::vector, deque) |
| CSubvector< Subiterator< _blasRep::iterator > > | |
| CSubvector< Subiterator< _Vector::Rep::iterator > > | |
| CSubvector< Subiterator< typename Rep::const_iterator > > | |
| CSubvector< Subiterator< typename Rep::iterator > > | |
| CSubvector< typename Rep::const_iterator > | |
| CSubvector< typename Rep::iterator, typename Rep::const_iterator > | |
| CSum< _Blackbox1, _Blackbox2 > | Blackbox of a matrix sum without copying |
| CSumOwner< _Blackbox1, _Blackbox2 > | Blackbox of a matrix sum without copying |
| CSylvester< _Field > | This is a representation of the Sylvester matrix of two polynomials |
| CPlotStyle::Term | What format the plot should be in? |
| CTernaryLattice | NO DOC |
| CPoint::Times | Y time |
| CTimeWatcher | Helper |
| CToeplitz< _CField, _PRing > | This is the blackbox representation of a Toeplitz matrix |
| CToeplitz< _Field > | |
| CToeplitz< typename _PRing::CoeffField, _PRing > | Specialization for when the field of matrix elements is the same as the coefficient field of the polynomial field |
| CTPL | Vector of triples |
| CTPL_omp | Triplesbb for openmp |
| CTraceCategory< BB > | Trait to show whether or not the BB class has a local trace function |
| CTranspose< Blackbox > | Transpose matrix without copying |
| CTranspose< LinBox::Submatrix< Blackbox > > | |
| CTransposedBlasMatrix< Matrix > | TransposedBlasMatrix |
| CTransposeMatrix< Matrix, Trait > | Matrix transpose |
| CTransposeMatrix< LinBox::Protected::SparseMatrixGeneric< _Field, _Row > > | |
| CTransposeMatrix< LinBox::Protected::SparseMatrixGeneric< _Field, Vector< _Field >::SparseMap > > | |
| CTransposeMatrix< LinBox::Protected::SparseMatrixGeneric< _Field, Vector< _Field >::SparsePar > > | |
| CTransposeMatrix< LinBox::Protected::SparseMatrixGeneric< _Field, Vector< _Field >::SparseSeq > > | |
| CTransposeOwner< Blackbox > | Transpose matrix without copying |
| CUniformTag | Iterator sampling uniformly from all primes of given bitsize |
| CUniqueSamplingTrait< IteratorTrait > | Whether a prime generator generates a sequence with non repeating numbers |
| CUnparametricRandIter< NTL::ZZ_p > | Constructor for random field element generator |
| CPoint::Values | Y |
| CVectorCategories | List of vector categories |
| CVectorFraction< Domain > | VectorFraction<Domain> is a vector of rational elements with common reduced denominator |
| CVectorFraction< Ring > | |
| ►CVectorStream< _Vector > | Vector factory |
| CConstantVectorStream< _Vector > | Constant vector factory |
| CRandomDenseStream< Field, _Vector, RandIter, Trait > | Random dense vector stream |
| CRandomDenseStream< Field, _Vector, RandIter, VectorCategories::DenseVectorTag > | Specialization of random dense stream for dense vectors |
| CRandomSparseStream< Field, _Vector, RandIter, Trait > | Random sparse vector stream |
| CRandomSparseStream< Field, _Vector, RandIter, VectorCategories::DenseVectorTag > | Specialization of RandomSparseStream for dense vectors |
| CRandomSparseStream< Field, _Vector, RandIter, VectorCategories::SparseAssociativeVectorTag > | Specialization of RandomSparseStream for sparse associative vectors |
| CRandomSparseStream< Field, _Vector, RandIter, VectorCategories::SparseParallelVectorTag > | Specialization of RandomSparseStream for sparse parallel vectors |
| CRandomSparseStream< Field, _Vector, RandIter, VectorCategories::SparseSequenceVectorTag > | Specialization of RandomSparseStream for sparse sequence vectors |
| CStandardBasisStream< Field, _Vector, Trait > | Stream for 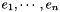 |
| CStandardBasisStream< Field, _Vector, VectorCategories::DenseVectorTag > | Specialization of standard basis stream for dense vectors |
| CStandardBasisStream< Field, _Vector, VectorCategories::SparseAssociativeVectorTag > | Specialization of standard basis stream for sparse associative vectors |
| CStandardBasisStream< Field, _Vector, VectorCategories::SparseParallelVectorTag > | Specialization of standard basis stream for sparse parallel vectors |
| CStandardBasisStream< Field, _Vector, VectorCategories::SparseSequenceVectorTag > | Specialization of standard basis stream for sparse sequence vectors |
| CVectorStream< BitVector > | |
| CVectorTraits< Vector > | Vector traits template structure |
| CWiedemannLiftingContainer< _Ring, _Field, _IMatrix, _FMatrix, _FPolynomial > | Wiedemann LiftingContianer |
| CWiedemannSolver< Field > | Linear system solvers based on Wiedemann's method |
| CZeroOne< _Field > | Time and space efficient representation of sparse {0,1}-matrices |
| CZeroOne< GF2 > | Time and space efficient representation of sparse matrices over GF2 |
| CZOQuad< _Field > | A class of striped or block-decomposed zero-one matrices |
 1.8.13
1.8.13