interface for solving linear system by p-adic lifting technique over the quotient field of a ring. More...

Collaboration diagram for p-adic lifting for linear system solutions.:

Data Structures
class	RationalSolver< Ring, Field, RandomPrime, MethodTraits >
	Interface for the different specialization of p-adic lifting based solvers. More...

Enumerations
enum	SolverReturnStatus
	define the different return status of the p-adic based solver's computation.

enum	SolverLevel
	Define the different strategy which can be used in the p-adic based solver. More...

Detailed Description

interface for solving linear system by p-adic lifting technique over the quotient field of a ring.

i.e. solution over the rational for an integer linear system.

See the following reference for details on this algorithm:

Robert T. Moenck and John H. Carter Approximate algorithms to derive exact solutions to system of linear equations. In Proc. EUROSAM'79, volume 72 of Lectures Note in Computer Science, pages 65-72, Berlin-Heidelberger-New York, 1979. Springer-Verlag.
John D. Dixon Exact Solution of linear equations using p-adic expansions. Numerische Mathematik, volume 40, pages 137-141, 1982.

Enumeration Type Documentation

Define the different strategy which can be used in the p-adic based solver.

Used to determine what level of solving should be done:

Monte Carlo: Try to solve if possible, but result is not guaranteed. In any case a 0 denominator should not be returned.
Las Vegas : Result should be guaranteed correct.
Certified : Additionally, provide certificates that the result returned is correct.
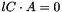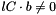
- if the return value is SS_INCONSISTENT, this means lastCertificate satisfies $lC \cdot A = 0$ and $lC \cdot b \neq 0$
- if diophantine solving was called and the return value is SS_OK, this means lastCertificate satisfies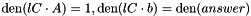 $\mathrm{den}(lC \cdot A) = 1, \mathrm{den}(lC \cdot b) = \mathrm{den}(answer)$