Introduction
LinBox is a C++ template library of routines for solution of linear algebra problems including linear system solution, rank, determinant, minimal polynomial, characteristic polynomial, and Smith normal form.
Algorithms are provided for matrices with integer entries or entries in a finite field. A number of matrix storage types is provided, especially for blackbox representation of sparse or structured matrix classes. A few algorithms for rational matrices are available. LinBox also uses underlying data structures and algorithms for integer, rational, polynomial, finite fields and rings, as well as dense and sparse matrix formats coming from the Givaro (https://casys.gricad-pages.univ-grenoble-alpes.fr/givaro) and FFLAS-FFPACK (http://linbox-team.github.io/fflas-ffpack) libraries.
Goals
Project LinBox (http://linalg.org) is a collaborative effort among researchers at a number of locations around the world. Some of the most active participants are listed here. The goals are to produce algorithms and software for symbolic linear algebra, particularly using blackbox matrix methods, i.e. iterative methods requiring only the linear transform property of the matrix (that, given A and x, one can compute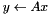 
). Such methods are especially effective with sparse or structured matrices for which the matrix-vector product can be computed cheaply. LinBox also provides elimination based methods for dense matrices exploiting the numeric BLAS routines via FFLAS-FFPACK.
A good collection of finite field implementations is available. Some algorithms are probabilistic, but their results are extremely reliable except over very small fields (less than 1000 elements, say).
Design
LinBox depends on other packages for some of its functionality. It is a design goal of LinBox to be a kind of middleware, providing a common interface for use in projects needing linear algebra and providing access to other systems and programs through wrappers whenever their capabilities may contribute to the linear algebra. Thus, to gain full advangage of LinBox it will be desirable to have certain other packages installed. In particular GMP and a BLAS implementation are required. GMP provides the basic large integer system used throughout. We have been using ATLAS for the BLAS implementation. The remaining dependencies are optional, but two packages stand out as contributing substantially to LinBox. They are NTL and Givaro. NTL is used for some finite field and ring representations, particularly in the case of GF(q), where q is a prime power or a prime greater than word size. NTL is also used by algorithms that need polynomial operations such as factorization. Givaro is another source of field representations and polynomial operations. Importantly, Givaro provides our best representation of small non-prime fields, say q = pe < 106. Functionality from some other systems has been wrapped also but is currently less widely used in LinBox.
Genericity and high performance are the twin goals of LinBox. The genericity is achieved by use of a small set of interfaces. Algorithms are implemented with C++ template parameters which may be instantiated with any class adhering to the specified interface. High performance is achieved by judicious specializations of the generic algorithms. It is entirely within the spirit of the project to introduce new implementations. Thus a user of the library may invoke a LinBox algorithm, say for determinant or rank of a matrix, but providing a blackbox class of her own design and perhaps even providing the underlying field (or commutative ring) representation. Conversely, the LinBox field and ring interfaces and the many specific representations can be used for purposes other than linear algebra computation or with algorithms not provided by LinBox.
Using LinBox
- Copyright and Licencing.
- LinBox tutorial. This is a brief introduction to LinBox capabilities.
- Installing LinBox. Explains how to install from sources or from the latest svn version.
- Architecture of the library. Describes how LinBox is organized
