examples/bigmat.C

Outputs a big and very sparse matrix.let C be the cyclic shift matrix with 1 on the 1,n position and along the first subdiagonal.

This matrix is 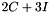. It has 2 nonzero entries per row and per column. It is an 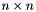matrix whose determinant is considerably less than the Hadamard bound (but is large – 3^n +- 2^n).

/*
 * examples/bigmat.C
 *
 * Copyright (C) 2007, 2010 B Youse, D. Saunders
 * ========LICENCE========
 * This file is part of the library LinBox.
 *
 * LinBox is free software: you can redistribute it and/or modify
 * it under the terms of the  GNU Lesser General Public
 * License as published by the Free Software Foundation; either
 * version 2.1 of the License, or (at your option) any later version.
 *
 * This library is distributed in the hope that it will be useful,
 * but WITHOUT ANY WARRANTY; without even the implied warranty of
 * MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the GNU
 * Lesser General Public License for more details.
 *
 * You should have received a copy of the GNU Lesser General Public
 * License along with this library; if not, write to the Free Software
 * Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA  02110-1301  USA
 * ========LICENCE========
 */


#include <iostream>
#include <cstdlib>
using namespace std;

int main(int argc, char* argv[])
{
    if (argc != 2 ) {
        cerr << "Usage: bigmat <n>, where <n> is the size you like." << endl;
        return -1;
    }

    int n = atoi(argv[1]);
    cout << n << " " << n << " M" << endl;
    cout << "1 1 3" << endl;
    cout << "1 " << n << " 2" << endl;
    for (int i = 2; i <=n; ++i)
    {
        cout << i << " " << i-1 << " " << 2 << endl;
        cout << i << " " << i << " " << 3 << endl;
    }
    cout << "0 0 0" << endl;
    return 0 ;
}

// Local Variables:
// mode: C++
// tab-width: 4
// indent-tabs-mode: nil
// c-basic-offset: 4
// End:
// vim:sts=4:sw=4:ts=4:et:sr:cino=>s,f0,{0,g0,(0,\:0,t0,+0,=s